Tugas Pra UAS
1. Sebutkan isi Pasal 1 ayat 1 UUD 1945.
Pasal 1(1) Negara Indonesia ialah negara kesatuan yang berbentuk Republik.(2) Kedaulatan adalah di tangan rakyat, dan dilakukan sepenuhnya oleh Majelis Permusyawaratan Rakyat.
2. Pemahaman Archipelago di Negara-Negara Barat berbeda dengan pemahaman Archipelago di Indonesia. Jelaskan tentang perbedaan tersebut.
- Perbedaan yang esensial dari pemahaman ini adalah bahwa menurut paham Barat, laut berperan sebagai “pemisah” pulau, sedangkan menurut paham Indonesia laut adalah “penghubung” sehingga wilayah Negara menjadi satu kesatuan yang utuh sebagai “Tanah Air” dan disebut Negara Kepulauan.
3. Indonesia telah meratifikasi UNCLOS 1982. Jelaskan apa keuntungan dan kerugiannya.
Keuntungan :
- diterimanya konsepsi negara kepulauan (Archipelagic State)
- ditetapkannya lebar laut wilayah (teritorial) 12 NM,
- batas zone ekonomi eksklusif (ZEE) 200 NM dan batas landas kontinen.
- pengakuan status Indonesia sebagai negara kepulauan secara formal
Kerugian :
- banyak nya kapal-kapal asing yang masuk ke perairan indonesia
- pada tahun 2004 menyebabkan kerugian US$ 2 bagi indonesia
- terjadiya ilegal Fishing
Label:
Kewarganegaraan
Ringkasan Aplikasi Presentasi
Kelompok 2
Nama Anggota:
1) Anggreini Reza Rahayu
2) Eko Haryanto
Kode Kelas : ML103A
Nama Dosen: Diah Aryani, ST.,M.Kom
Gambar diatas adalah menu utama dari aplikasi yang kita punya
ini adalah menu dari aplikasi yang pilih di tab pada menu statistic.
Ini adalah Tampilan dari menu Tutorial, Tutorial adalah penjelasan dari beberapa pengertian dalam arti yang secara luas.
ini adalah penjelasan-penjelasan dari menu tutorial--> introduction. disini kita bisa mengetahui apakah pengertian statistik dan apa saja metode-metode yang harus digunakan.
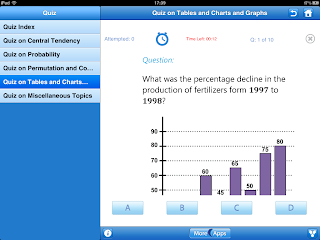
ini adalah tampilan dari menu quiz, quiz fungsinya adalah mengukur seberapa pengertian kita dalam teori yang telah di jelaskan di dalam menu Tutorial tersebut, disini pun terdapat pilihan jawaban dan waktu untuk menjawab, dan quiz ini pun dapat di share melalui: email, facebook dan twitter, quiz ini berisi kan 10 pertanyaan. jika kita ingin mencoba quiz yang lain,kita harus membayar aplikasi tersebut.
ini adalah tampilan dari Flash Card, Flash Card adalah rangkuman dari beberapa penjelasan yang ada di dalam introduction dan juga terdapat beberapa rumus didalam flash card ini.
Label:
Statistik Deskriptif
Artikel statistik
1.1. Pengertian statistik dan statistika
Statistik adalah kumpulan data, bilangan maupun non bilangan yang disusun
dalam table dan atau diagram yang melukiskan suatu persoalan
Tabel nilai statistika
Nilai Jumlah Mahasiswa
A 5
B 9
C 25
D 3
E 1
Statistika adalah pengetahuan yang berhubungan dengan cara-cara pengumpulan data,
pengolahan atau penganalisaannya dan penarikan kesimpulan berdasarkan kumpulan data
dan penganalisaan yang dilakukan.
Statistika dikelompokkan dalam dua kelompok yaitu:
statistika deskriptif dan statistika inferensia.
Statistika deskriptif adalah metode yang berkaitan dengan pengumpulan dan penyajian suatu gugus data sehingga memberikan informasi yang berguna. Sedangkan pengertian statistika inferensia adalah metode yang berhubungan dengan analisis sebagian data untuk kemudian sampai pada peramalan atau penarikan kesimpulan tentang seluruh gugus data induknya.
1.2. Data Statistik
Data statistik adalah keterangan atau ilustrasi mengenai sesuatu hal yang bisa
berbentuk kategori (misalnya rusak, baik, cerah, berhasil) atau bilangan. Selanjutnya data
yang berupa kategori disebut sebagai data kualitatif dan data bilangan disebut data
kuantitatif. Berdasarkan cara perolehannya data kuantitatif dibedakan menjadi data
diskrit dan data kontinu. Data-data yang diperoleh dari hasil menghitung atau membilang
termasuk dalam data diskrit, sedangkan data-data yang diperoleh dari hasil mengukur
termasuk dalam data kontinu.
Menurut sumbernya kita mengenal data intern dan data ekstern.
Data intern adalah data yang diperoleh dari perusahaan atau instansi yang bersangkutan. Sedangkan
data ekstern diperoleh dari luar instansi atau perusahaan tersebut.
Data ekstern dibedakan menjadi data primer dan data sekunder.
Data primer adalah data yang dikeluarkan oleh badan sejenis. Sedangkan data lainnya termasuk data
sekunder. Semua data-data yang beru dikumpulkan dan belum pernah diolah disebut
sebagai data mentah.
1.3. Populasi dan sampel
Populasi adalah keseluruhan pengamatan yang menjadi perhatian kita baik yang
berhingga maupun tak berhingga jumlahnya. Seringkali tidak praktis mengambil data dari
keseluruhan populasi untuk menarik suatu kesimpulan. Untuk itu dilakukan pengambilan
sampel yaitu sebagian atau himpinan bagian dari populasi. Sampel yang diambil haris
dapat merepresentasikan populasi yang ada. Prosedur pengambialan sampel yang
menghasilkan kesimpulan yang konsisten terlalu tinggi atau terlalu rendah mengenai
suatu ciri populasi dikatakan berbias. Untuk menghindari kemungkinan bias ini perlu
dilakukan pengambian contoh acak atau contoh acak sederhana. Contoh acak sederhana
didefinisikan sebagai contoh yang dipilih sedemikian rupa sehingga setiap himpunan
bagian yang berukuran n dari populasi mempunyai peluang terpilih yang sama.
Dalam perhitungan dan analisis data statistik seringkali diperlukan pembulatan
angka-angka. Berikut ini adalah beberapa aturan tentang pembulatan angka-angka.
1. Jika angka yang harus dihilangkan adalah 4 atau kurang, maka angka terkanan yang
mendahuluinya tetap.
Contoh: Rp. 59.376,- dibulatkan menjadi Rp. 59 ribu.
2. Jika angka yang haarus dihilangkan adalah lebih dari 5 atau angka 5 diikuti angka
bukan nol maka angka yang mendahuluinya ditambah dengan 1.
Contoh: 176,51 kg dibulatkan menjadi 177 kg.
3. Jika angka yang harus dihilangkan hanya angka 5 atau angka 5 diikuti nol, maka
angka yang mendahuluinya tetap jika genap dan ditambah 1 jika ganjil.
Contoh: 8,500 dibulatkan menjadi 8
19,5 dibulatkan menjadi 20
1.5. Penyajian Data
Secara garis besar ada dua macam cara penyajian data dalam statistika yaitu:
1. Tabel atau daftar yang dapat berbentuk:a. Daftar baris kolom
b. Daftar kontingensi
c. Daftar distribusi frekuensi
2. Grafik atau diagram yang terbagi menjadi:
a. Diagram batang atau balok
b. Diagram garis atau grafik
c. Diagram lingkaran
d. Diagram lambing
e. Diagram peta
f. Diagram pencar
1.6. Daftar distribusi frekuensi dan grafiknya
Dalam distribusi frekuensi data dikelompokkan dalam beberapa kelas interval misalnya
a–b, c-d dan seterusnya. Ada beberapa istilah yang digunakan dalam distribusi frekuensi
yaitu:
1.
Limit kelas atau ujung kelas yaitu nilai-nilai terkecil dan terbesar dalam setiap
kelas interval. Nilai terbesar disebut sebagai limit atas kelas dan nilai terkecil
disebut sebagai limit bawah kelas.
2.
Batas kelas yaitu limit kelas ± setengah nilai skala terkecil. Nilai yang besar
disebut batas atas kelas dan nilai yang kecil disebut sebagai batas bawah kelas.
3.
Titik tengah kelas atau tanda kelas yaitu nilai yang terletak pada engah setiap kelas
interval. Aturan umum yang digunakan untuk menentukan titik tengah kelas atau
tanda kelas adalah:
Tanda kelas = ± 1⁄2 (limit bawah + limit atas)
Macam-macam distribusi frekuensi
1. Distribusi frekuensi
2. Distribusi frekuensi. Relative (%)
3. Distribusi frekuensi kumulatif kurang dari
4. Distribusi frekuensi kumulatif lebih dari
1.7. CARA MEMBUAT DIST. FREK.
1. Tentukan Rentang
R = Nilai terbesar – nilai terkecil.
= 99 - 35 = 64
2. Tentukan banyaknya kelas interval.
Acuan aturan Starges
Banyak kelas
= 1 + (3,3) log n
= 1 + (3,3) log 80 = 7,28
≈ 7 kelas
3. Tentukan panjang kelas interval
P=
Re n tan g
64
=
= 9,14 = 10 Banyakkelas7
4. Tentukan limit kelas
5. Daftar semua limit keats
6. Menentukan frekwensi → bantuan kolom tabulasi
Contoh:
Nilai Ujian Statistik 80 orang mahasiswa adalah sebagai berikut:
79 49 48 34 81 98 87 80
80 84 90 70 91 93 82 78
70 71 92 38 56 81 74 73
68 72 85 51 65 93 83 86
80 35 83 73 74 43 86 88
92 93 76 71 90 72 67 75
80 91 61 72 97 81 88 81
70 74 98 95 80 59 73 71
83 60 83 82 60 67 89 63
76 63 88 70 66 88 79 75
Dengan menggunakan aturan pembuatan distribusi frekuensi tersebut di atas dapat dibuat
sebuah distribusi frekuensi dengan 7 kelas sebagai berikut:
Nilai Ujian
31 – 40
41 – 50
51 – 60
61 – 70
71 – 80
81 – 90
91 - 100
Frekuensi (f)
2
3
5
14
24
20
12
1.8. Model Populasi
Adalah pendekatan bentuk polygon frekuensi dengan garis lengkung halus yang
bentuknya secocok mungkin:
a. Model normal
b. Model simetrik
c. Model miring (ke kanan/ke kiri).
Jika suatu frekwensi tidak simetrik maka nilai mean (rata-rata) dan median tidak sama.
Koefisien ke menjuluran pearson (sk)
sk =
3(μ -μ
σ
μ = median
μ = mean (rata-rata)
σ = simpangan baku.
TUGAS I :
Berikut ini adalah data daya tahan alat terhadap suatu insektisida dalam satuan menit.
2.4 0.7 3.9 2.8 1.3
1.6 2.9 2.6 3.7 2.1
3.2 3.5 1.8 3.1 0.3
4.6 0.9 3.4 2.3 2.5
0.4 2.1 2.5 1.5 4.3
1.8 2.4 1.3 2.6 1.8
2.7 0.4 2.8 3.5 1.4
1.7 3.9 1.1 5.9 2.0
5.3 6.3 0.2 2.0 1.9
1.2 2.5 1.2 1.2 1.7
Dengan menggunakan 8 kelas interval dan nilai terendah 0,1
a. Buat distribusi frekuensi, distribusi frekuensi relatif (%) dan distribusi frekuensi
kumulatif
b. Dengan menggunakan Microsoft Exel buatlah
1. Diagram balok, histogram, polygon frekuensi, Ogif dan diagram
lingkaran.
2. Tentukan rata-rata (mean), modus, median, kuartil dan desil.
1.9. UKURAN PEMUSATAN
Ukuran pemusatan dibagi dalam dua kelompok
1. Ukuran gejala pusat, meliputi
• Rata-rata hitung (mean)
• Rata-rata ukur
• Rata-rata harmonic
• Rata-rata gabungan
• Modus
2. Ukuran letak, meliputi
• Median
• Kuartil
• Desil
• Persentil
Ukuran-ukuran tersebut di atas dapat dihitung dari kumpulan data populasi atau sampel.
Jika ukuran-ukuran yang diambil dihitung dari data populasi disebut
parameter ,
sedangkan jika dihitung dari data sampel disebut statistic.
1.9.1. Rata-rata Hitung (Mean)
Diperoleh dengan membagi jumlah seluruh data dengan banyak data
x=
∑x
i
n
Jika masing-masing mempunyai frekuensi maka rata-ratanya disebut sebagai rata-rata
terboboti.
x=
∑f x
∑f
i
i
i
contoh;
Disimpan (fi)
Barang
% Rusak (xi)
fi xi
A 100 96 96
B 200 46 92
C 160 50 80
D 80 75 60
Berapa persen rata-rata barang yang rusak
x=
∑f x
∑f
i
i
i
=
328
x 100 % = 60,07 %
540
Bukan seperti ini
x=
(96% + 46% + 50% + 75%) = 66,75 %
4
1.9.2. Rata-rata Gabungan
Jika kita mempunyai data n1, n2, n3, ... dengan nilai rata-rata masing-masing x 1 , x 2 , x 3 , ...
maka rata-rata gabungan data di atas dinyatakan dengan
x gab =
∑n x
∑n
i
i
i
Untuk data-data yangv tersusun dalam distribusi frekuensi rata-ratanya dihitung dengan
x=
∑f x
∑f
k
k
k
dengan xk : nilai tengah kelas
fk : frekuensi kelas
atau dengan cara singkat/sandi (khusus untuk lebar kelas yang sama) yakni sebagai
berikut
∑ fi ci
x = xo + p
∑f
i
dengan xo : tengah kelas acuan
fi : frekuensi ke-i
ci : harga sandi
p : lebar kelas
1.9.3 Rata-rata Ukur (geometrik)
Digunakan jika perbandingan dua data berturutan tetap atau hampir tetap.
U = n x 1 . x 2 . x 3 ... x n
Untuk bilangan-bulangan yang besar digunakan
log U =
∑ log x
i
n
Untuk fenomena yang bersifat tumbuh seperti pertumbuhan penduduk, bakteri dan lain-
lain digunakan
x
Pt = Po 1 +
100
t
Untuk data-data yang telah disusun dalam daftar distribusi frekuensi rata-rata ukurnya
dinyatakan
log U =
∑ (f log x )
∑f
i
i
i
1.9.4. Rata-rata Harmonik
Rata-rata harmonik biasanya digunakan untuk merata-ratakan kecepatan beberapa jarak
tempuh atau mencari harga rata-rata suatu komoditi tertentu.
H=
n
1
∑ x
i
Untuk data-data yang disusun dalam distribusi frekuensi
H=
∑f
i
fi
i
∑ x
Secara umum hubungan rata-rata hitung (x ) , rata-rata ukur (U) dan rata-rata harmonic
(H) dinyatakan
H≤U≤x
1.9.5. MODUS
Modus adalah nilai atau fenomena yang paling sering muncul jika datanya telah disusun
dalam distribusi frekuensi .
b1
Mo = b + p
b +b
2
1
dengan b : batas bawah kelas modal (kelas dengan frekuensi tertinggi)
p : panjang/lebar kelas modal
b1: frekuensi kelas modal dikurangi frekuensi kelas sebelumnya
b2: frekuensi kelas modal dikurangi frekuensi kelas sebelumnya
1.9.6. KUARTIL
Jika sekumpulan data dibagi menjadi empat bagian yang sama setelah di urutkan maka
nilai yang membaginya disebut kuartil.
Letak k i = data ke
i (n + 1)
; i = 1, 2, 3
4
Untuk data yang disusun dalam distribusi frekuensi
in
−F
; i = 1, 2, 3
K i = b + p 10
f
dengan b : batas bawah kelas Di
p : panjang kelas Di
F : jumlah seluruh frekuensi sebelum kelas Di
f : frekuensi kelas Di
1.9.7. PRESENTIL
Jika sekumpulan data dibagi 100 sama besar akan menghasilkan persentil ke 1,2,3,...,99.
Letak Pi = data ke
i (n + 1)
100
Untuk data dalam distribusi frekuensi
in
− F
100
Pi = b + p
f
dengan b : batas bawah kelas Pi
p : panjang kelas Pi
F : jumlah seluruh frekuensi sebelum kelas Pis
f : frekuensi kelas Pi
QUIZ I
1. Apa yang dimaksud data diskrit dan data kontinu. Berikan masing-masing dua
contoh!
2. Jelaskan perbedaan diagram batang dan histogram. Gambarkan sketsanya!
3. Bagaimana rumus aturan untuk menentukan banyak kelas interval. Beri
keterangan symbol-simbolnya.
4. Berikut adalah data umur 100 karyawan pabrik
44
35
41
31
49
34
37
63
51
33
37
33
41
38
52
31
40
36
42
28
40
40
35
32
45
39
40
48
61
61
44
58
53
47
30
64
31
35
65
43
67
53
42
43
52
68
64
46
50
45
59
56
59
47
43
37
52
40
27
44
41
33
29
24
47
26
45
41
55
34
51
58
34
26
25
44
57
67
59
62
28 44 31 29 53 41 52 36 51 40
40 31 52 56 58 58 52 23 35 52
a. Buat daftar distribusi frekuensi dengan 5 kelas.
b. Gambarkan polygon frekuensinya.
c. Tentukan mean, modus, median
Kuartil 1 dan desil 7 berdasarkan distribusi fekuensi yang telah dibuat.
1.10. UKURAN SIMPANGAN
Ukuran simpangan digunakan sebagai gambaran bagaimana berpencarnya suatu
data kuantitatif. Ukuran-ukuran tersebut yaitu:
a. Rentang = data terbesar – data terkecil
b.Rentang Antar Kuartil (RAK)
RAK = K3 – K1
c. Simpangan Kuartil (SK)
= 1/2 RAK = 1/2 (K3 – K1)
SK
d. Rata-rata Simpangan (RS)
RS
=
∑
χi − χ
n
Selalu positif
e. Simpangan baku/ deviasi standart
•
Simpangan baku untuk sampel disimbolkan S
•
Simpangan baku untuk populasi disimbolkan σ
Kuadrat simpangan baku disebut Varians
Varians sampel dihitung dengan :
2
S
= ∑ (χ
− χ)
= n ∑ χ i − (∑ χ i )
2
i
n −1
atau
2
2
2
S
Ini lebih dianjurkan karena kesalahannya -
n (n − 1 )
Lebih kecil
Jika datanya dalam distribusi frekuensi :
2
S
= ∑ f (χ
= n ∑ f i χ i − (∑ f i χ i )
i
− χ)
2
i
n −1
Atau
2
2
2
S
n (n − 1 )
Cara Sandi xi dapat diganti ci
Simpangn baku gabungan
S2
=
∑ (n − 1)S
∑n−K
i
2
i
ni = jumlah data sampel ke i
Si = Simpangan baku sample ke i
K = jumlah / banyaknya sampel .
Bilangan baku/ Nilai Z
Bilangan baku/nilai z didefinisikan sebagai :
Zi
=
∑χ
i
−χ
s
; i = 1,2,3,.... N
Atau lengkapnya
Zi
χi − χ
s
= χo + s o
xo = rata-rata bilangan baku
so = Simpangan baku
Ukuran-ukuran
simpangan diatas merupakan ukuran absolut. Jika dari simpangan
absolut diambil simpangan bakunya, maka kita dapat koefisien Variasi
KV
=
Simpangan baku
x100%
rata - rata
Selain ukuran simpangan/ disperse absolut, dikenal pula dispersi relatif yang dinyatakan :
Dispersi relative
=
Simpangan baku
rata - rata
Label:
Statistik Deskriptif
Quiz meeting 11
Which of the following is the main topic of the passage?
Answer: C. The current American family
C. The current American family
D. The ideal family
C. The current American family
D. The ideal family
2. The word current in paragraph 2 could best be replaced by which of the following?
Answer: B. Present
A. Typical
B. Present
C. perfect
D. Traditional
3. The word none in paragraph 2 refers to
Answer: B. children
A. parents
B. children
C. couples
D. families
4. How many single people were identified in the survey?
Answer: C. One fifth of the total surveyed
A. One third of the total surveyed
B. One fourth of the total surveyed
C. One fifth of the total surveyed
D. Less than one tenth of the total surveyed
5.Who generally constitutes a one-person household?
Answer: C. A single woman in her late sixties
A. A single man in his twenties
B. An elderly man
C. A single woman in her late sixties
D. A divorced woman
6.The word undervalues in paragraph 4 is closest in meaning to?
Answer: A. does not appreciate
A. does not appreciate
B. does not know about
C. does not include
D. does not understand
7. The passage discusses all of the following reasons for an increase in single- parent households EXCEPT
Answer: C. increased interest in parenting by fathers
A. a rising divorce rate
B. death of one of the parents
C. increased interest in parenting by fathers
D. babies born to single women
8. With which of the following statements would the author most probably agree?
Answer: A. There have always been a wide variety of family arrangements in the United States
A. There have always been a wide variety of family arrangements in the United States
B. Racial, ethnic, and religious groups have
preserved the traditional family structure
C. The ideal American family is the best structure
D. Fewer married couples are having children
Answer: C. The current American family
C. The current American family
D. The ideal family
C. The current American family
D. The ideal family
2. The word current in paragraph 2 could best be replaced by which of the following?
Answer: B. Present
A. Typical
B. Present
C. perfect
D. Traditional
3. The word none in paragraph 2 refers to
Answer: B. children
A. parents
B. children
C. couples
D. families
4. How many single people were identified in the survey?
Answer: C. One fifth of the total surveyed
A. One third of the total surveyed
B. One fourth of the total surveyed
C. One fifth of the total surveyed
D. Less than one tenth of the total surveyed
5.Who generally constitutes a one-person household?
Answer: C. A single woman in her late sixties
A. A single man in his twenties
B. An elderly man
C. A single woman in her late sixties
D. A divorced woman
6.The word undervalues in paragraph 4 is closest in meaning to?
Answer: A. does not appreciate
A. does not appreciate
B. does not know about
C. does not include
D. does not understand
7. The passage discusses all of the following reasons for an increase in single- parent households EXCEPT
Answer: C. increased interest in parenting by fathers
A. a rising divorce rate
B. death of one of the parents
C. increased interest in parenting by fathers
D. babies born to single women
8. With which of the following statements would the author most probably agree?
Answer: A. There have always been a wide variety of family arrangements in the United States
A. There have always been a wide variety of family arrangements in the United States
B. Racial, ethnic, and religious groups have
preserved the traditional family structure
C. The ideal American family is the best structure
D. Fewer married couples are having children
Label:
English For IT 2
Subscribe to:
Comments (Atom)